Expressions
Now that we have support for identifiers and literals, we can start adding support for expressions. We cannot talk about expressions without talking about operators and operator precedence. Nim's approach to operators is unique, as it treats operators as regular procedures. This means that we can define our own operators using any combination of operator symbols. There are three types of operators:
- Unary operators: operators that take one argument and can be written in prefix notation (e.g.,
-a). - Binary operators: operators that take two arguments and can be written in infix notation (e.g.,
a + b). - Operators that take more than two arguments, which can only be used as a proc call (e.g.
`*+`(a, b, c)).
Examples:
let
a = 40 # literal
b = a # identifier
c = a + 2 # binary expression
d = -c # unary expression
e = 2 + 4 * 10 # operator precedence (* has higher precedence than +)
f = (2 + 4) * 10 # parentheses can be used to change precedence
g = true # boolean literal
h = not g # unary boolean expression
i = g and h # binary boolean expression
j = i or (e < f) # boolean expression using relational operators
In addition to typical expressions like arithmetic and logical operations, Nim supports block expressions, which are expressions that contain a block of code, where the value of the block is the value of the last expression in the block.
Examples:
let
a = block: # block expression
echo "Hello"
42
b = if a > 50: a else: a + 10 # if expression
c = case a: # case expression
of 0: "zero"
of 42: "forty-two"
else: "not forty-two"
We'll come back to block expressions later, but for now, let's start with the basics.
Nim Operators
Operators in Nim can be defined using any combination of the following operator symbols:
= + - * / < >
@ $ ~ & % |
! ? ^ . : \
An exception is made for the following set since these are used for other purposes in the language:
.(member access, method call syntax)=(assignment, initialization):(type declaration, block start)::(seems to be reserved for future use)..(slice or range operator)
There's also a predefined set of keyword operators:
and or not xor shl shr div mod in notin is isnot of as from
Special patterns of operators affect the operator precedence:
- operators that start with a
.are called dot-like operators - operators that start with a
@are called sigil-like operators - operators that end with
->,~>or=>are called arrow-like operators - operators that end with
=and their first character is not one of<,>,!,=,~,?are called assignment operators
Here's a modified version of the operator precedence table from the Nim manual:
| Precedence Level | Operators | First character | Trailing character(s) | Terminal symbol |
|---|---|---|---|---|
| 10 (highest) | $ ^ | OP10 | ||
| 9 | * / % div mod shl shr | * / % \ | OP9 | |
| 8 | + - | + -, |, ~ | OP8 | |
| 7 | & | & | OP7 | |
| 6 | dot-like operator (e.g. .?) .. | . | OP6 | |
| 5 | == <= < >= > !=in notin is isnot not of as from | = < > ! | OP5 | |
| 4 | and | OP4 | ||
| 3 | or xor | OP3 | ||
| 2 | @ : ? | OP2 | ||
| 1 | assignment operator (e.g. +=, *=) | not one of:< > ! = ~ ? | = | OP1 |
| 0 (lowest) | arrow-like operator (e.g. ->, =>) | -> ~> => | OP0 |
Lexing Operators
Let's apply the above operator rules to recognize operators. We'll classify them into the 11 precedence levels mentioned above, from OP0 to OP10. There's also a couple of things we need to address:
- we'll need to make sure that the five exceptions mentioned above are handled separately, since they cannot be combined with other operator symbols
- we'll need to consider the assignment operators when matching certain cases, since it changes the precedence level of the operator to
OP1
// src/main/kotlin/khaledh/nimjet/lexer/Nim.flex
...
{%
...
private IElementType considerAssign(IElementType type) {
// if the last character is '=', then it's an assignment operator
return yycharat(yylength() - 1) == '=' ? NimToken.OP1 : type;
}
}%
...
Opr = [=+\-*/<>@$~&%|!?\^\.:\\]
NotOpr = [^=+\-*/<>@$~&%|!?\^\.:\\]
%%
...
<DEFAULT> {
...
// special tokens: `=`, ':', '::', '.', '..'
"=" / {NotOpr} { return NimToken.EQ; }
":" / {NotOpr} { return NimToken.COLON; }
"::" / {NotOpr} { return NimToken.COLONCOLON; }
"." / {NotOpr} { return NimToken.DOT; }
".." / {NotOpr} { return NimToken.DOTDOT; }
// operators have 11 precendence levels (0 to 10)
{Opr}*?[\-~=]">" { return NimToken.OP0; }
[@:\?]{Opr}* { return NimToken.OP2; }
[=<>!]{Opr}* { return NimToken.OP5; }
\.{Opr}+ { return considerAssign(NimToken.OP6); }
\&{Opr}* { return considerAssign(NimToken.OP7); }
\~{Opr}* { return NimToken.OP8; }
[+\-|]{Opr}* { return considerAssign(NimToken.OP8); }
[*%/\\]{Opr}* { return considerAssign(NimToken.OP9); }
[$\^]{Opr}* { return considerAssign(NimToken.OP10); }
// keyword operators
"or" { return NimToken.OP3; }
"xor" { return NimToken.OP3; }
"and" { return NimToken.OP4; }
"in" { return NimToken.OP5; }
"notin" { return NimToken.OP5; }
"is" { return NimToken.OP5; }
"isnot" { return NimToken.OP5; }
"not" { return NimToken.OP5; }
"of" { return NimToken.OP5; }
"as" { return NimToken.OP5; }
"from" { return NimToken.OP5; }
"div" { return NimToken.OP9; }
"mod" { return NimToken.OP9; }
"shl" { return NimToken.OP9; }
"shr" { return NimToken.OP9; }
...
}
The Opr regex matches any operator symbol, while NotOpr does the opposite. We use the NotOpr regex in first set of rules (using the lookahead / operator), the five special cases, to ensure that these tokens are not followed by another operator symbol (which would make them part of a different operator).
In the second set of rules, we use the Opr regex to match the different kinds of operators based on leading and/or trailing symbols, and return their precedence level token. Some of these rules call the considerAssign utility function to check if the last character is an equals sign, which makes the operator an assignment operator (thus returning OP1 instead of the original precedence level). Notice that we split the case of OP8 into two rules: the one with a ~ prefix shouldn't consider assignment operators, while the one with the +, -, or | prefixes should (as per the Nim manual).
In the third set of rules, we match the predefined keyword operators and return their corresponding precedence level.
We have a bit of a problem though. The .. operator should be recognized as an OP6 token, since it's an operator with that precedence level. However, it's also going to be used in other places in the grammar. Since we can't use two different tokens for the same lexeme, we'll have to handle this in the parser. Instead of returning OP6 from the lexer, we'll define an OP6 rule in the grammar that matches any token from that precedence level. The only other lexer rule with that precedence level is the dot-like operator rule, so we'll give it a different token name, DOT_LIKE. Then we can combine DOTDOT and DOT_LIKE in the parser under the OP6 rule.
<DEFAULT> {
// turned into OP6 in the grammar
".." / {NotOpr} { return NimToken.DOTDOT; }
...
// turned into OP6 in the grammar
\.{Opr}+ { return considerAssign(NimToken.DOT_LIKE); }
}
Now, let's turn our attention to the grammar.
Parsing Expressions
Parsing expressions in recursive descent parsers usually requires implementing a function for each precedence level, which delegates to the next higher precedence level to parse its operands, and keeps parsing until it encounters an operator with a lower precedence level. This has a couple of issues: first, the grammar must not be left-recursive, otherwise the parser will go into an infinite loop; and second, recursive implementation can be slow for deeply nested expressions (not to mention the risk of stack overflow).
Fortunately, Grammar-Kit has built-in support for parsing expressions using an optimized approach that avoids these issues. All we need to do is define our expression rules in the order of precedence levels (from lowest to highest), and have each rule extend the root expression rule.
Let's start by adding the new expression rules to the grammar.
{
...
extends(".+Expr")=SimpleExpr
}
...
// Expressions
Expr ::= SimpleExpr
SimpleExpr ::= Op0Expr
| Op1Expr
| Op2Expr
| Op3Expr
| Op4Expr
| Op5Expr
| Op6Expr
| Op7Expr
| Op8Expr
| Op9Expr
| Op10Expr
| PrimaryExpr
Op0Expr ::= SimpleExpr OP0 SimpleExpr
Op1Expr ::= SimpleExpr OP1 SimpleExpr
Op2Expr ::= SimpleExpr OP2 SimpleExpr
Op3Expr ::= SimpleExpr OP3 SimpleExpr
Op4Expr ::= SimpleExpr OP4 SimpleExpr
Op5Expr ::= SimpleExpr OP5 SimpleExpr
Op6Expr ::= SimpleExpr OP6 SimpleExpr
Op7Expr ::= SimpleExpr OP7 SimpleExpr
Op8Expr ::= SimpleExpr OP8 SimpleExpr
Op9Expr ::= SimpleExpr OP9 SimpleExpr
Op10Expr ::= SimpleExpr OP10 SimpleExpr
PrimaryExpr ::= Literal | IdentRef
// Operators
private OP6 ::= DOTDOT | DOT_LIKE
A few notes on the rules:
- The starting rule is
Expr, which is the root rule for all expressions. Currently, it only includesSimpleExpr, but it will include block expressions later. - The
SimpleExprrule matches any of the 11 precedence level rules, as well as primary expressions. - Each precedence level rule is a binary expression that matches two operands and an operator of the corresponding precedence level.
- Notice that we use the
SimpleExprrule as the operand type, which allows for recursive parsing of expressions. This leads to left recursion, which is handled by Grammar-Kit's optimized expression parsing. For this to work properly, we make all rules that end inExprextendSimpleExprusing theextendsdirective. - The
PrimaryExprrule simply matches either a literal or an identifier reference (for now). - The
OP6rule combines theDOTDOTandDOT_LIKEtokens into a single rule, as mentioned earlier.
Time to test everything out.
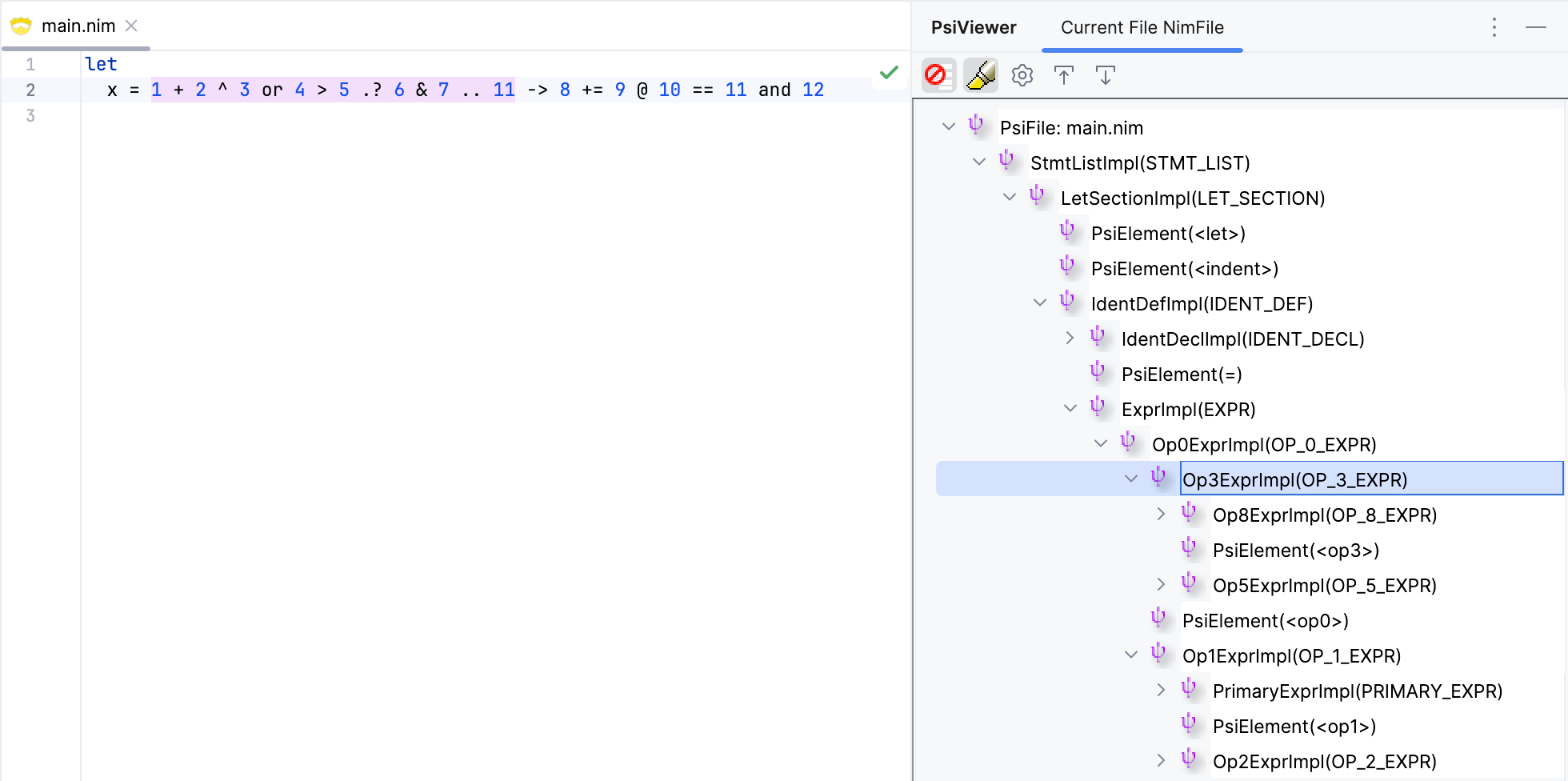
For testing, I used an expression that includes most of the operators and precedence levels. The result looks good, with the expression being parsed correctly. Since it's hard to see the entire expression tree from the screenshot, I have included a textual representation below.
┌────────────────────── -> ───┐
┌────── or ──┐ ┌ += ──┐
┌ + ──┐ ┌ > ────────────┐ 8 ┌ @ ──────────┐
1 ┌ ^ ┐ 4 ┌─────── .. ─┐ 9 ┌──── and ─┐
2 3 ┌ .? ──┐ 11 ┌─ == ─┐ 12
5 ┌ & ┐ 10 11
6 7
x = 1 + 2 ^ 3 or 4 > 5 .? 6 & 7 .. 11 -> 8 += 9 @ 10 == 11 and 12
Unary Operators
Nim also supports unary operators, or prefix operators as they're called in the manual:
Whether an operator is used as a prefix operator is also affected by preceding whitespace.
So, a unary operator has leading whitespace, but no trailing whitespace; e.g., in echo $foo the $ is a unary operator, while in let c = a $ b the $ is a binary operator. Note that, in a$ b and a$b the $ is also a binary operator.
While we can recognize unary operators in the lexer, this will double the number of operator tokens we have to handle in the parser. A simpler approach is to customize the parser to recognize if an operator is unary based on the surrounding whitespace.
Fortunately, Grammar-Kit supports adding custom methods to the parser as an escape hatch, which can be invoked using the <<method>> notation in the grammar. Those are called external rules. We can use this feature to call into a method that checks if an operator is unary. Let's start by adding a parser utility class that will handle this.
// src/main/kotlin/khaledh/nimjet/parser/NimParserUtil.kt
...
class NimParserUtil : GeneratedParserUtilBase() {
companion object {
...
@JvmStatic
@Suppress("UNUSED_PARAMETER")
fun isUnary(builder: PsiBuilder, level: Int): Boolean {
var leading = (
builder.currentOffset > 0 &&
builder.originalText[builder.currentOffset - 1].isWhitespace()
)
var trailing = builder.tokenText?.let {
builder.currentOffset + it.length < builder.originalText.length &&
builder.originalText[builder.currentOffset + it.length].isWhitespace()
} == true
return leading && !trailing
}
}
}
Note: The @Suppress("UNUSED_PARAMETER") annotation is used to suppress the warning about the unused level parameter (this is just the parser level, which we don't need). We use the builder parameter to get the current token type and advance the lexer when needed.
The method should be self-explanatory. We make use of the currentOffset and originalText properties of the PsiBuilder to check if the character before and after the token is whitespace. We then return true if the operator has leading whitespace but no trailing whitespace.
Let's add the external rule to the grammar and use it to handle unary operators.
{
...
parserUtilClass="khaledh.nimjet.parser.NimParserUtil"
...
}
...
PrimaryExpr ::= Literal
| IdentRef
| PrefixExpr
PrefixExpr ::= OP_UNARY PrimaryExpr
// Operators
private OP6 ::= DOTDOT | DOT_LIKE
private OP ::= OP0 | OP1 | OP2 | OP3 | OP4 | OP5 | OP6 | OP7 | OP8 | OP9 | OP10
private OP_UNARY ::= <<is_unary>> OP
...
// external rules
external is_unary ::= isUnary
We first tell Grammar-Kit to use the NimParserUtil class for the parser utilities (i.e. external rules). The external rules are declared at the end using the external directive by assigning the rule name to the corresponding method in the parser utility class.
We added a private OP rule that matches any operator, and an OP_UNARY rule that uses the <<is_unary>> external rule to check if the operator is unary.
The PrefixExpr rule matches a unary operator followed by a PrimaryExpr. This rule itself is a case of the PrimaryExpr rule, since it binds stronger than binary expressions.
Sigil-like Operators
Another special case for unary operators is the sigil-like operators, i.e. those that start with the @ symbol. From the Nim manual:
If a unary operator's first character is
@it is a sigil-like operator which binds stronger than aprimarySuffix:@x.abcis parsed as(@x).abcwhereas$x.abcis parsed as$(x.abc).
We are not tackling the primarySuffix rule yet, but we can still handle those sigil-like operators in order to be ready for when we do. Even though the Nim manual refers to them as unary operators, in the actual implementation they are allowed to have trailing whitespace for some reason (maybe it was an oversight?).
Let's split the OP2 token into two tokens, OP2_SIGIL_LIKE and OP2_OTHER, and add a rule in the parser to group them under an OP2 rule.
[@:\?]{Opr}* { return NimToken.OP2; }
@{Opr}* { return NimToken.OP2_SIGIL_LIKE; }
[:\?]{Opr}* { return NimToken.OP2_OTHER; }
Sigil-like operators are allowed to appear before identifier and literals. Let's update the grammar to reflect this.
...
Op0Expr ::= SimpleExpr OP0 <<expr_ind>> SimpleExpr
Op1Expr ::= SimpleExpr OP1 <<expr_ind>> SimpleExpr
Op2Expr ::= SimpleExpr OP2_OTHER <<expr_ind>> SimpleExpr
...
PrimaryExpr ::= OP2_SIGIL_LIKE? Literal
| OP2_SIGIL_LIKE? IdentRef
| PrefixExpr
| ParenExpr
...
// Operators
private OP2 ::= OP2_SIGIL_LIKE | OP2_OTHER
...
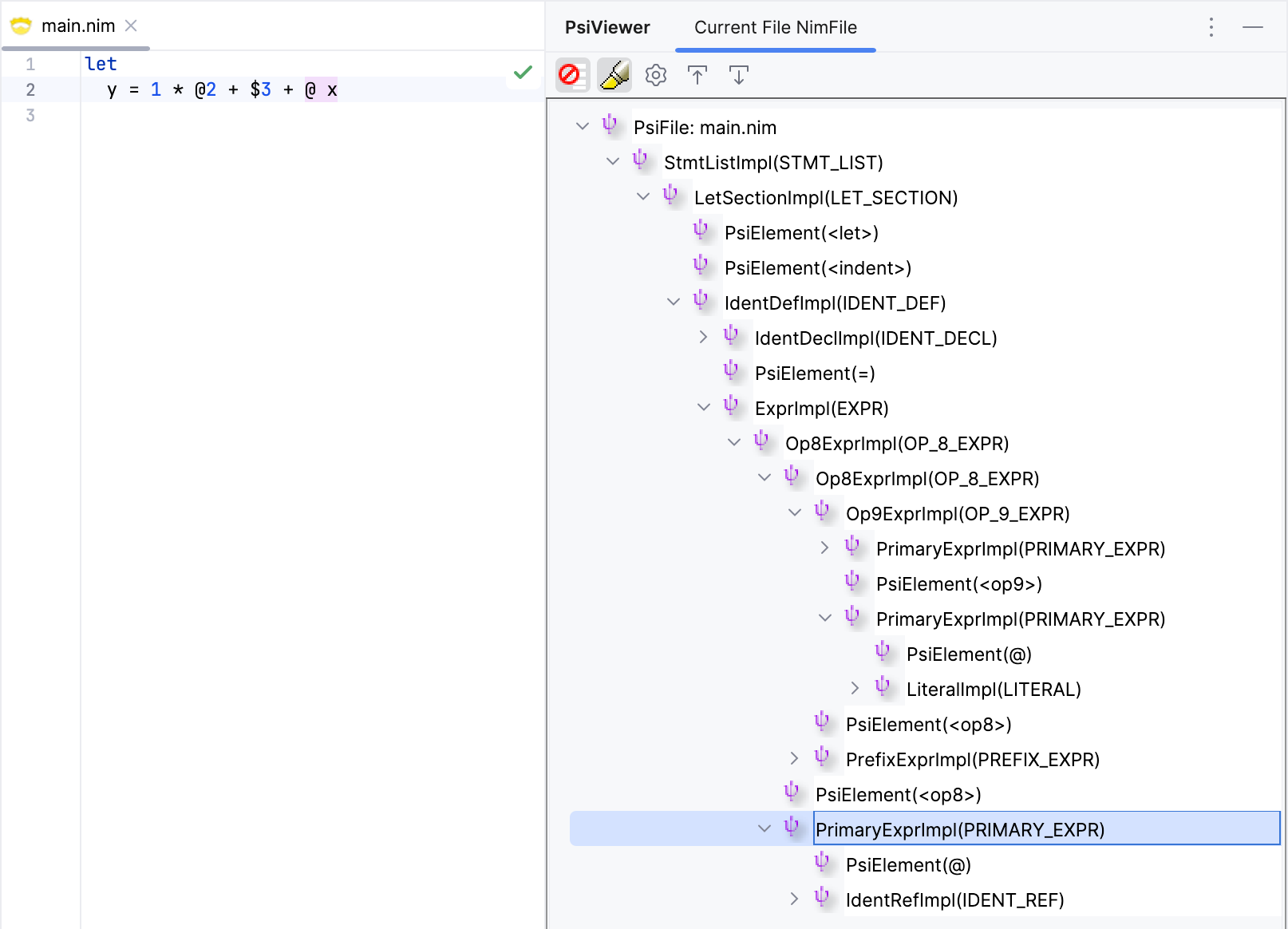
The sigil-like operator is parsed correctly. It is treated as a unary operator, even if it has trailing whitespace.
Parentheses
Parentheses are used to group expressions and change the order of evaluation. They have higher precedence than any binary operator, and can be nested. They're usually considered a form of primary expression.
Let's first add the opening and closing parentheses tokens to the lexer.
...
<DEFAULT> {
...
"(" { return NimToken.LPAREN; }
")" { return NimToken.RPAREN; }
...
}
Now, let's add the parentheses rule to the grammar.
...
PrimaryExpr ::= Literal
| IdentRef
| PrefixExpr
| ParenExpr
PrefixExpr ::= OP_UNARY PrimaryExpr
ParenExpr ::= LPAREN SimpleExpr RPAREN
...
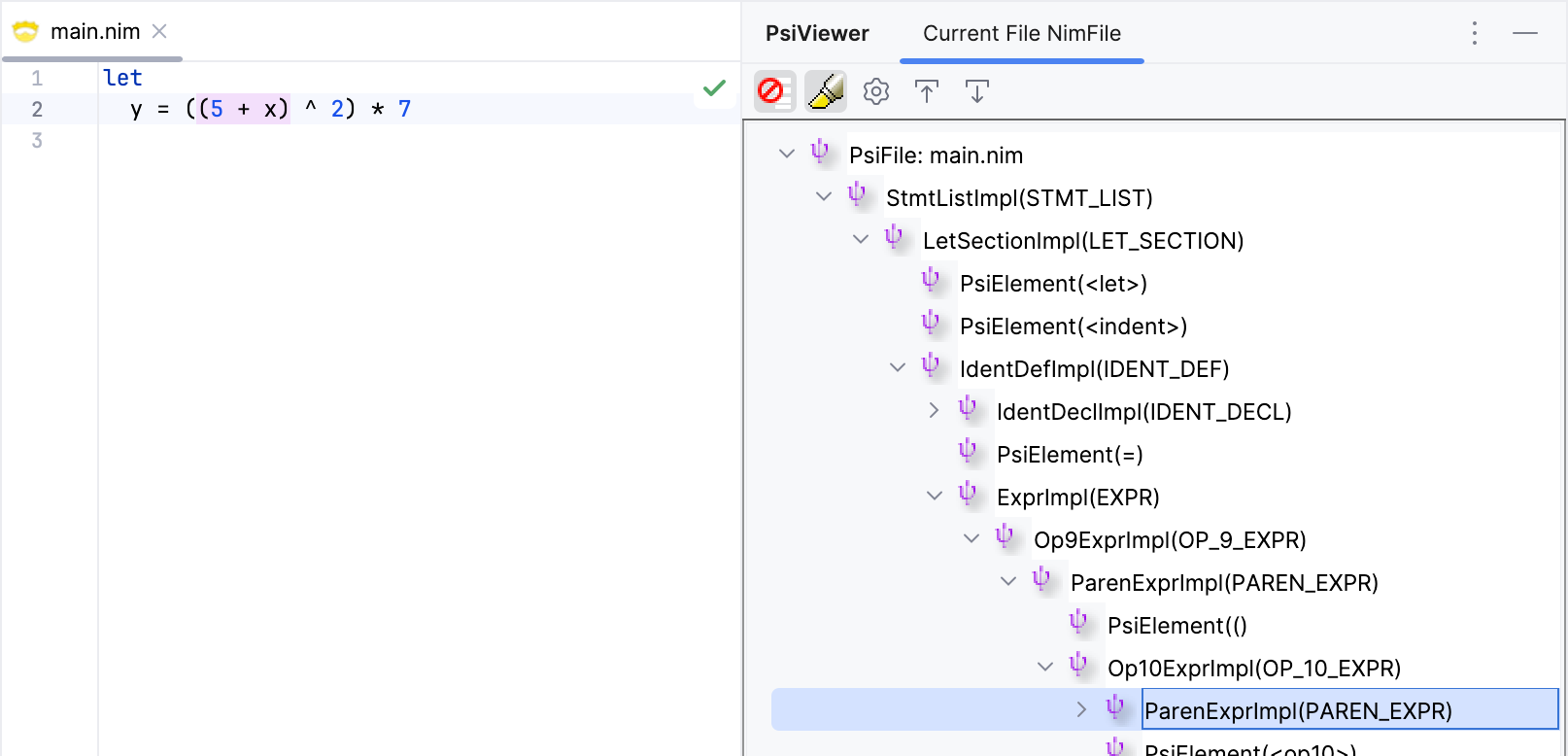
Looks good. We have two nested parentheses expressions, and they are parsed with the correct precedence, overriding the default precedence of the operators.
Right Associativity
One final thing to consider is right-associative operators. In Nim, the only right-associative operator starts with the ^ symbol. From the manual:
Binary operators whose first character is
^are right-associative, all other binary operators are left-associative.proc `^/`(x, y: float): float = # a right-associative division operator result = x / y echo 12 ^/ 4 ^/ 8 # 24.0 (4 / 8 = 0.5, then 12 / 0.5 = 24.0) echo 12 / 4 / 8 # 0.375 (12 / 4 = 3.0, then 3 / 8 = 0.375)
Fortunately, Grammar-Kit supports right-associative operators through the rightAssociative rule attribute. Right now, operators starting with ^ are grouped with those starting with $ under the same precedence level, OP10. We'll need to update the lexer to recognize them separately, and then use each in a separate rule in the grammar.
[$\^]{Opr}* { return considerAssign(NimToken.OP10); }
[$]{Opr}* { return considerAssign(NimToken.OP10_DOLLAR); }
[\^]{Opr}* { return considerAssign(NimToken.OP10_CARET); }
Let's update the grammar to reflect this change.
...
SimpleExpr ::= Op0Expr
| Op1Expr
...
| Op10Expr
| Op10LeftExpr
| Op10RightExpr
| PrimaryExpr
Op0Expr ::= SimpleExpr OP0 <<expr_ind>> SimpleExpr
Op1Expr ::= SimpleExpr OP1 <<expr_ind>> SimpleExpr
...
Op10Expr ::= SimpleExpr OP10 <<expr_ind>> SimpleExpr
Op10LeftExpr ::= SimpleExpr OP10_DOLLAR <<expr_ind>> SimpleExpr
Op10RightExpr ::= SimpleExpr OP10_CARET <<expr_ind>> SimpleExpr {rightAssociative=true}
...
// Operators
private OP2 ::= OP2_SIGIL_LIKE | OP2_OTHER
private OP6 ::= DOTDOT | DOT_LIKE
private OP10 ::= OP10_DOLLAR | OP10_CARET
private OP ::= OP0 | OP1 | OP2 | OP3 | OP4 | OP5 | OP6 | OP7 | OP8 | OP9 | OP10
private OP_UNARY ::= <<is_unary>> OP
Let's see if it works.
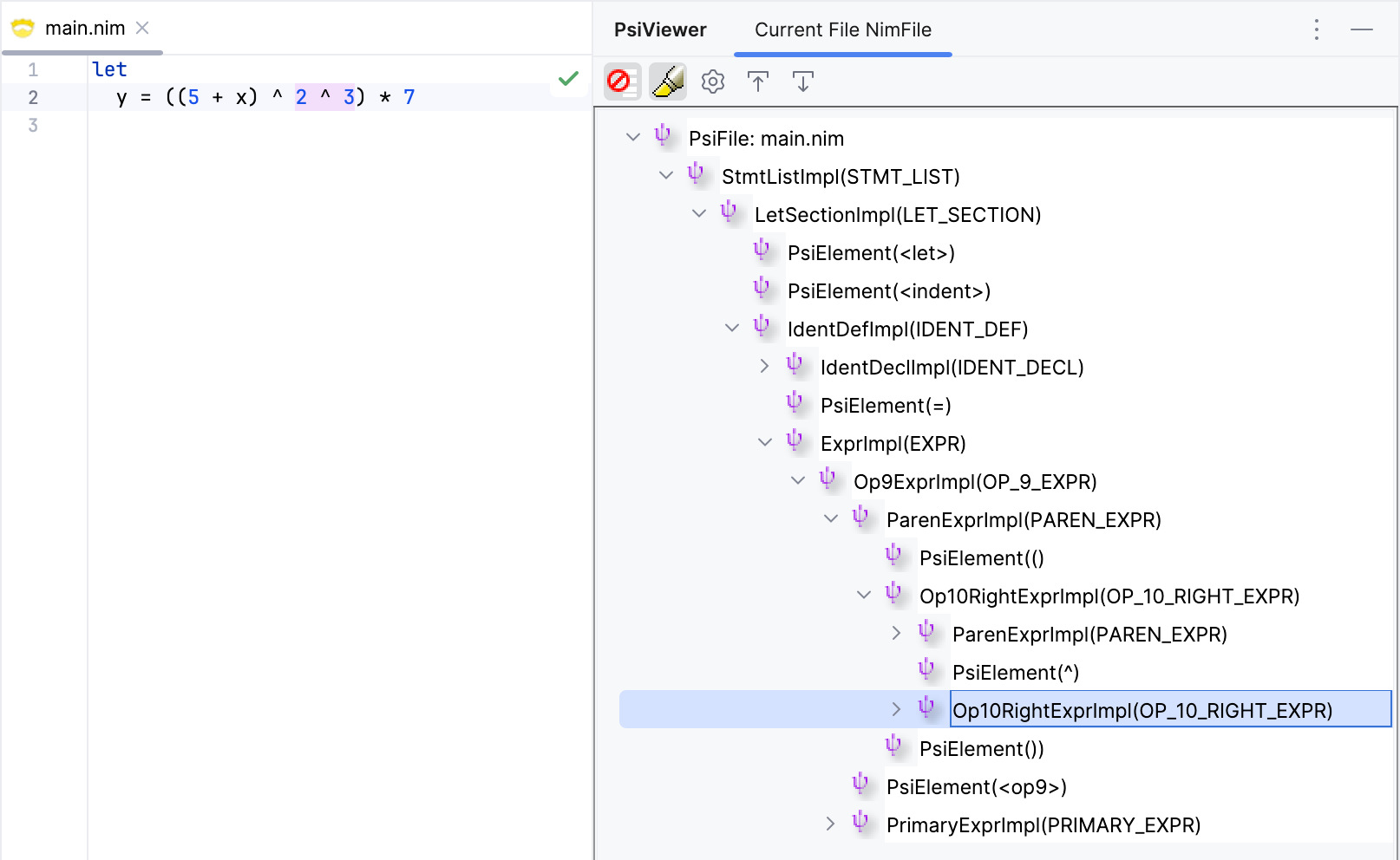
The right-associative operator is parsed correctly. The expression (5 + x) ^ 2 ^ 3 is parsed as (5 + x) ^ (2 ^ 3), as expected (the second ^ operator has higher precedence than the first one).
Handling Indentation
Nim supports a flexible indentation format within expressions. Unlike structured indentation of code blocks (which requires every indent to have a corresponding dedent), expressions can have indents, equal indents, and dedents after any operator in an expression. For example, the above expression can be written as follows:
let
x = 1 + 2 ^
3 or 4 > 5 .? 6 &
7 .. 11 ->
8 += 9 @
10 == 11 and
12
This poses a challenge for us, since there's no pattern for the indentation inside an expression that we can capture through a grammar rule. A naive approach would be to update the expression rules to allow any number of indentation tokens (including none) to appear after an operator. The issue with this approach is that, after an expression ends, we can't tell how many dedent tokens we need to skip to get back to the correct indentation level. We need a way to track the indentation level in the parser.
Let's add a few external rules to the parser utility class to handle this.
...
class NimParserUtil : GeneratedParserUtilBase() {
companion object {
private var exprIndentLevel = 0
@JvmStatic
@Suppress("UNUSED_PARAMETER")
fun exprIndentStart(builder: PsiBuilder, level: Int): Boolean {
exprIndentLevel = 0
return true
}
@JvmStatic
@Suppress("UNUSED_PARAMETER")
fun exprIndent(builder: PsiBuilder, level: Int): Boolean {
if (builder.tokenType == NimToken.IND) {
exprIndentLevel++
builder.advanceLexer()
} else {
while (builder.tokenType == NimToken.DED && exprIndentLevel > 0) {
exprIndentLevel--
builder.advanceLexer()
}
if (builder.tokenType == NimToken.EQD) {
builder.advanceLexer()
}
}
return true
}
@JvmStatic
@Suppress("UNUSED_PARAMETER")
fun exprIndentEnd(builder: PsiBuilder, level: Int): Boolean {
while (builder.tokenType in setOf(NimToken.DED, NimToken.EQD) && exprIndentLevel > 0) {
if (builder.tokenType == NimToken.DED) {
exprIndentLevel--
}
builder.advanceLexer()
}
return true
}
...
}
}
We declare an exprIndentLevel variable to track the current indentation level in an expression. We define three methods:
exprIndentStart: resets theexprIndentLevelto 0 at the start of an expressionexprIndent: has two cases:- If the current token is
IND, it increments theexprIndentLeveland advances the lexer to the next token - Otherwise, it consumes any
DEDtokens (if any) while decrementing theexprIndentLeveland advancing the lexer. After consuming anyDEDtokens, it checks if the next token isEQDand simply advances the lexer if it is. This consumes any equal indents that might appear after an operator. Remember that dedents can be followed by an equal indent if the dedents bring the indentation level to the same level as a previous indentation.
- If the current token is
exprIndentEnd: similar to the second case ofexprIndent, but it consumes any remainingDEDtokens (if any) after the expression ends. It doesn't consumeEQD(if any) since such a token would belong to the parent block, not the expression.
The idea here is to call exprIndentStart at the start of an expression, exprIndent after any operator within the expression, and exprIndentEnd at the end of the expression. Let's modify the grammar to use these external rules.
...
Expr ::= <<expr_ind_start>> SimpleExpr <<expr_ind_end>>
...
Op0Expr ::= SimpleExpr OP0 <<expr_ind>> SimpleExpr
Op1Expr ::= SimpleExpr OP1 <<expr_ind>> SimpleExpr
...
Op10Expr ::= SimpleExpr OP10 <<expr_ind>> SimpleExpr
...
// external rules
...
external expr_ind_start ::= exprIndentStart
external expr_ind ::= exprIndent
external expr_ind_end ::= exprIndentEnd
We then use the <<expr_ind_start>> and <<expr_ind_end>> rules at the start and end of the Expr rule, respectively. This ensures that the indentation level is reset at the beginning of an expression and that any leftover dedent tokens are consumed at the end.
Finally, we use the <<expr_ind>> rule after each operator in the expression rules. This takes care of tracking indentation changes within the expression.
Let's try it out.
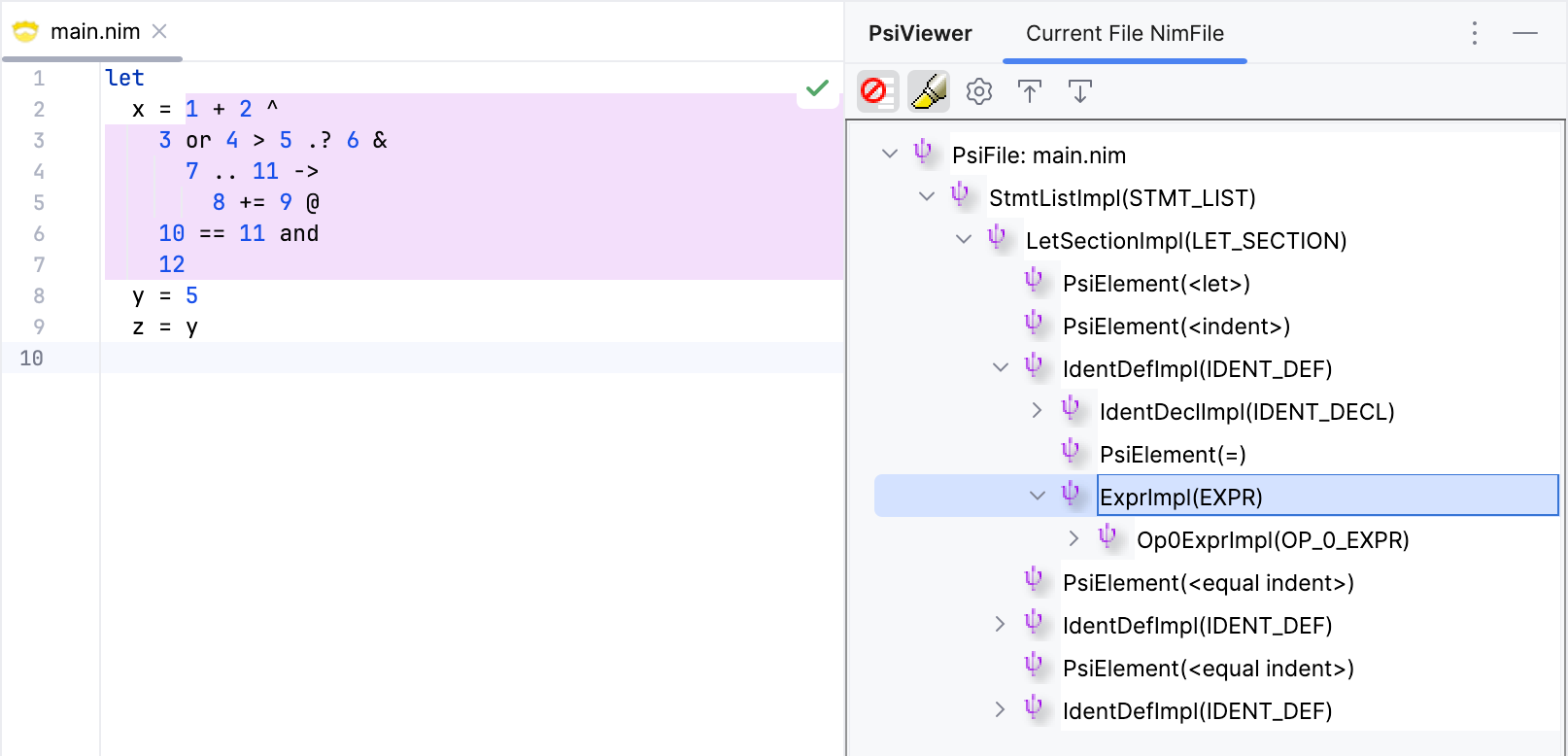
It seems to work as expected. The expression is parsed correctly, and the declaration following it are also parsed correctly.
This has been a long section. We've covered a lot of ground: operator precedence, binary and unary operators (including some special cases), right-associative operators, and handling indentation within expressions. We still need to handle block expressions, but for now we've got basic expressions under our belt.